图像基础知识总结

一、卷积在数字图像处理中应用

1）什么是卷积

      用一个模板和一幅图像进行卷积，对于图像上的一个点，让模板的原点和该点重合，然后模板上的点和图像上对应的点相乘，然后各点的积相加，就得到了该点的卷积值。对图像上的每个点都这样处理。由于大多数模板都是对称的，所以模板不旋转。  

卷积示例：
            

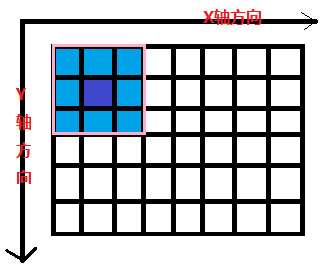
          3 * 3 的像素区域R与卷积核G的卷积运算：
              R5(中心像素)=R1G1 + R2G2 + R3G3 + R4G4 + R5G5 + R6G6 + R7G7 + R8G8 + R9G9
            

卷积是一种线性运算,图像处理中常见的mask运算都是卷积,广泛应用于图像滤波。高斯变换就是用高斯函数对图像进行卷积。

2）卷积的作用

     利用卷积可以实现对图像模糊处理、平滑处理，边缘检测，产生轧花效果的图像。

一个简单的数字图像卷积处理流程可以如下：

1.      读取源图像像素

2.      应用卷积操作数矩阵产生目标图像

3.      对目标图像进行归一化处理

4.      处理边界像素

3.常用模板：

二、傅里叶变换

    傅立叶变换在这里的物理意义就是将光的空间分布转换为频率分布（相空间），在靠近原点的部分为图像低频部分，远离原点部分为图像高频部分。

1）那么变换后高频部分对应图像的哪一部分呢？

         因为傅立叶变换并非一一对应的，频率空间上任何一处，哪怕只有一点都与原来的整幅图像有关，也就是说，这是非局域性的。

举个例子，全息图，任取全息图的一部分还原（做一次逆傅立叶变换）成的图像都是原来的整幅图像，但由于高频信息的缺失所以还原图像比原图像要模糊。

从物理效果看，傅立叶变换是将图像从空间域转换到频率域，其逆变换是将图像从频率域转换到空间域。换句话说，傅立叶变换的物理意义是将图像的灰度分布函数变换为图像的频率分布函数，傅立叶逆变换是将图像的频率分布函数变换为灰度分布函数

三、滤波

均值滤波对于高斯噪声的效果比较好

中值滤波对于椒盐噪声的效果比较好